Revised version 2017.
Published version 2005.
Original posted version 2004.

Abstract

This article is an introduction to the theory of Shimura varieties or, in other words, the arithmetic theory of automorphic functions and holomorphic automorphic forms. In the revised version, the numbering is unchanged from the original published version except for displays.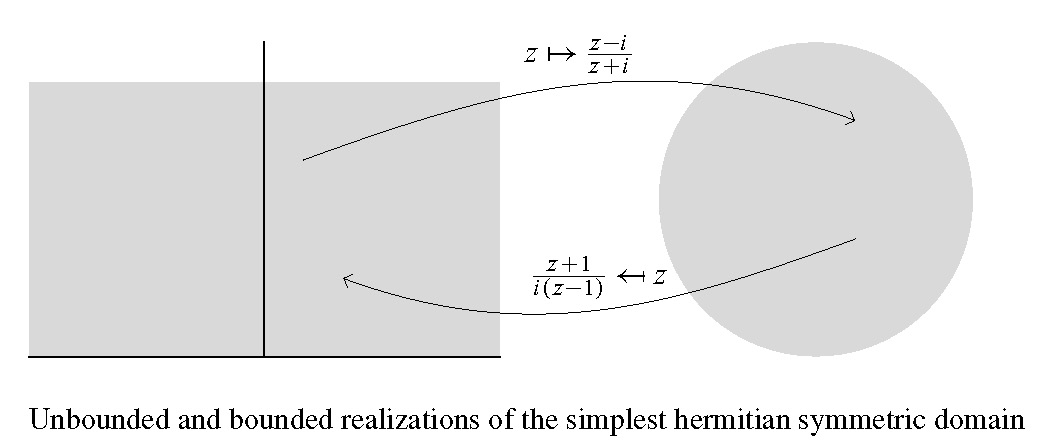

Contents

Hermitian symmetric domains; Hodge structures and their classifying spaces; locally symmetric varieties; connected Shimura varieties; Shimura varieties; the Siegel modular variety; Shimura varieties of Hodge type; PEL Shimura varieties; general Shimura varieties; complex multiplication (the Shimura-Taniyama formula and the main theorem); definition of canonical models; uniqueness of canonical models; existence of canonical models; abelian varieties over finite fields; the good reduction of Shimura varieties; a formula for the number of points. Appendices: complements; list of Shimura varieties of abelian type; review of Shimura's collected works.

About

These are my notes for a series of fifteen lectures at the Clay Summer School, Fields Institute, Toronto, June 2 -- June 27, 2003. The original version was published as: Introduction to Shimura varieties, In Harmonic Analysis, the Trace Formula and Shimura Varieties (James Arthur, Robert Kottwitz, Editors) 265--378, Clay Math. Proc., 4, Amer. Math. Soc., Providence, RI 2005. The notes were revised in 2017.

Introduction to the revised version (2017)

On looking at these notes thirteen years after they were written, I found that they read too closely as being my personal notes for the lectures. In particular, they lacked the motivation and historical background that (I hope) the lectures provided. In revising them, I have added this background, and I have fixed all the errors and instances of careless writing that have been pointed out to me. Unnumbered asides are new, and this version includes three appendices not in the published version.

One point I should emphasize is that this is an introduction to the theory of general Shimura varieties. Although Shimura varieties of PEL-type form a very important class --- they are the moduli varieties of abelian varieties with polarization, endomorphism, and level structure --- they make up only a small class in the totality of Shimura varieties.

The theory of Shimura varieties originated with the theory elliptic modular curves. My notes Modular Functions and Modular Forms emphasize the arithmetic and the geometry of these curves, and so provide an elementary preview of some of the theory discussed in these notes.

The entire foundations of the theory of Shimura varieties need to be reworked. Once that has been accomplished, perhaps I will write a definitive version of the notes.

Added March 25, 2021. I explain the last statement.

• The existence of canonical models for Shimura varieties of abelian type should be proved as in my 1994 article Seattle2 instead of as in Deligne's Corvallis article.
• The proof of the existence of canonical models in the general case should be based on Nori-Raghunathan 1989/93 rather than Kazhdan, and the proof of the canonical model of the standard principal bundle should be proved at the same time.
• The definition of "Shimura variety" should be generalized slightly to allow for the varieties showing up in boundaries.

Comment on Shimura, May 14, 2019.

Throughout his career Shimura followed a very independent path --- no one seems to know who his doctoral advisor was. The elliptic modular curves (quotients of the complex upper half plane by a congruence subgroup of $\mathrm{SL}(2,\mathbb{Z}))$ are initially defined over the complex numbers, but they are known to have canonical models over number fields. The analysts prove this by using the properties of the Fourier expansions at the cusps, and the algebraic geometers prove it by recognizing the curve as a moduli variety. There are similar complex curves attached to any quaternion algebra over $\mathbb{Q}$ split over $\mathbb{R}$, but they have no cusps and are not moduli varieties, and so no one suspected they also had canonical models, until Shimura proved they did. His result was initially met with disbelief by both the analysts and the geometers. This was perhaps his most original contribution, and was not something that someone too deeply embedded in the culture of the day could come up with. The curves are now called Shimura curves.